Acausality in Classical Physics

This is from John D. Norton, Causation as Folk Science

Even quite simple Newtonian systems can harbor uncaused events and ones for which the theory cannot even supply probabilities. Due to such systems ordinary Newtonian mechanics cannot license a principle or law of causality.

The Mass on the Dome#

Consider the dome that has a radial coordinate \(r\) and is rotationally symmetric about the origin \(r=0\), which is also the highest point of the dome. The shape of the dome is given by \(h=(2/3g)r^{3/2}\), how far the dome surface lies below its highest point as a function of the radial coordinate in the surface \(r\). Here \(g\) is gravity.

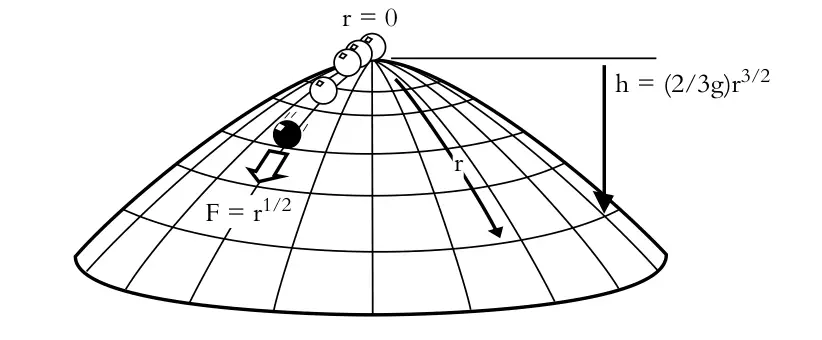
Now a point-like unit mass slides frictionlessly over the surface under the action of gravity. The magnitude of the gravitational force tangential to the surface at any point is
 

\[F=\frac{d(gh)}{dr} = r^{½}\]

so that Newton's second law sets the radial acceleration to be
 

\[\frac{d^2 r}{dt^2} = r^{½}.\]

Suppose that the mass is initially located at rest at the apex \(r=0\), then there is one obvious solution \(r(t) = 0\), but there is another large class of unexpected solutions. For any \(T\geq 0\) an arbitrarily chosen constant,
 

\[r(t) = \begin{cases} (1/144)(t-T)^4 & t\geq T\\ 0 & t\leq T\end{cases}\]

is a solution. The point mass sits at rest at the apex of the dome, and at an arbitrary time \(t=T\) it spontaneously moves off in some arbitrary radial direction.

Newton's First Law#

It may be objected that spontaneous acceleration violates Newton's first law:

In the absence of a net external force. a body remains at rest or in a state of uniform motion in a straight line.

But at just one instant, the law corresponds to motion with zero acceleration, so the instantaneous form of Newton's first law should be

In the absence of a net external force, a body is unaccelerated.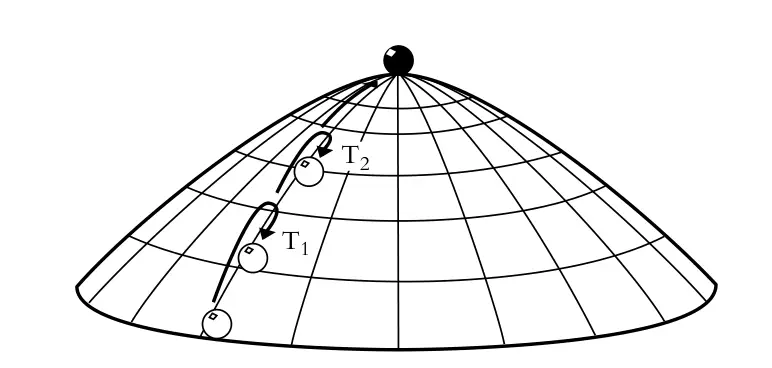

Now:

• For \(t\leq T\), there is no force, and the mass is unaccelerated. At \(t=T\), specifically \(a(t) = 0\).
• For \(t> T\), there is a net force applied, since the body is at positions \(r>0\) not at the apex.

The moment \(t=T\) is, instead of the first instant at which the mass moves, the last instant at which the mass does not move. Any candidate first instant in \(t>T%, say\), \(t=T+\epsilon\) with any \(\epsilon >0\), will be preceded by an earlier one, \(t=T+\epsilon/2\). There is no first instant of motion and thus no first instant at which to seek the initiating cause.

This can be understood by imagining the motion of the point mass that initiates its motion at the bottom and when reaches the apex its velocity becomes \(0\).