Fourier Series
Fourier series of periodic functions#
Definition. If \(f:\mathbb{R} \to \mathbb{R}\) is periodic with period \(2\pi\) and integrable over \([-\pi,\pi]\), the \(n\)-th Fourier coefficients \(c_n\) of \(f\) is defined as
\[c_n = \frac{1}{2\pi} \int_{-\pi}^{\pi} f(\theta) e^{-in\theta}d\theta.\]The corresponding series
\[\sum e_n e^{in\theta}\]is called the Fourier series of \(f\).
The choice of the interval \([-\pi,\pi]\) for integration is arbitrary, since we have the following obvious lemma:
Lemma. If \(F\) is periodic with period \(P\), then \(\int_a^{a+P} F(x) dx\) is independent of \(a\).
Convergence of Fourier series of periodic functions#
Estimates on the Fourier coefficients#
We have the following estimate on the Fourier coefficients:
Bessel's inequality. If \(f\) is \(2\pi\)-perioidc and Riemann integrable on \([-\pi,\pi]\), then the Fourier coefficients \(c_n\) of \(f\) satisfies
\[\sum |c_n|^2 \leq \frac{1}{2\pi}\int_{-\pi}^\pi |f(\theta)|^2 d\theta.\]This means that the series \(\sum |c_n|^2\) is convergent. As a consequence we have the following result, which is a special case of the Riemann-Lebesgue lemma,
Proposition. The Fourier coefficients \(c_n \to 0\) as \(n\to \infty, -\infty\).
Piecewise continuity#
Given a function \(f\) on a closed interval \([a,b]\), it is said to be pointwise continuous provided that \(f\) is continuous on \([a,b]\) except at finitely many points \(x_1,\ldots,x_k\), and that at each of the points \(x_1,\ldots x_k\), the left- and right- hand limits of \(f\) exist (for endpoints, if they are one of the points \(x_1,\ldots, x_k\), we require the existence of appropriate one limit). We denote the class of ponitwise continuous functions on \([a,b]\) with \(PC([a,b])\). The class of piecewise \(C^1\) functions will be denoted by \(PC^1\), etc.
A function is piecewise continuous or \(C^1\) on \(\mathbb{R}\) if it is on every bounded interval.
The Dirichlet kernels#
The sum of any infinite series is defined to be the limit of its partial sums. Hence, if \(f\sim\sum c_n e^{in\theta}\) converges, it is the limit of
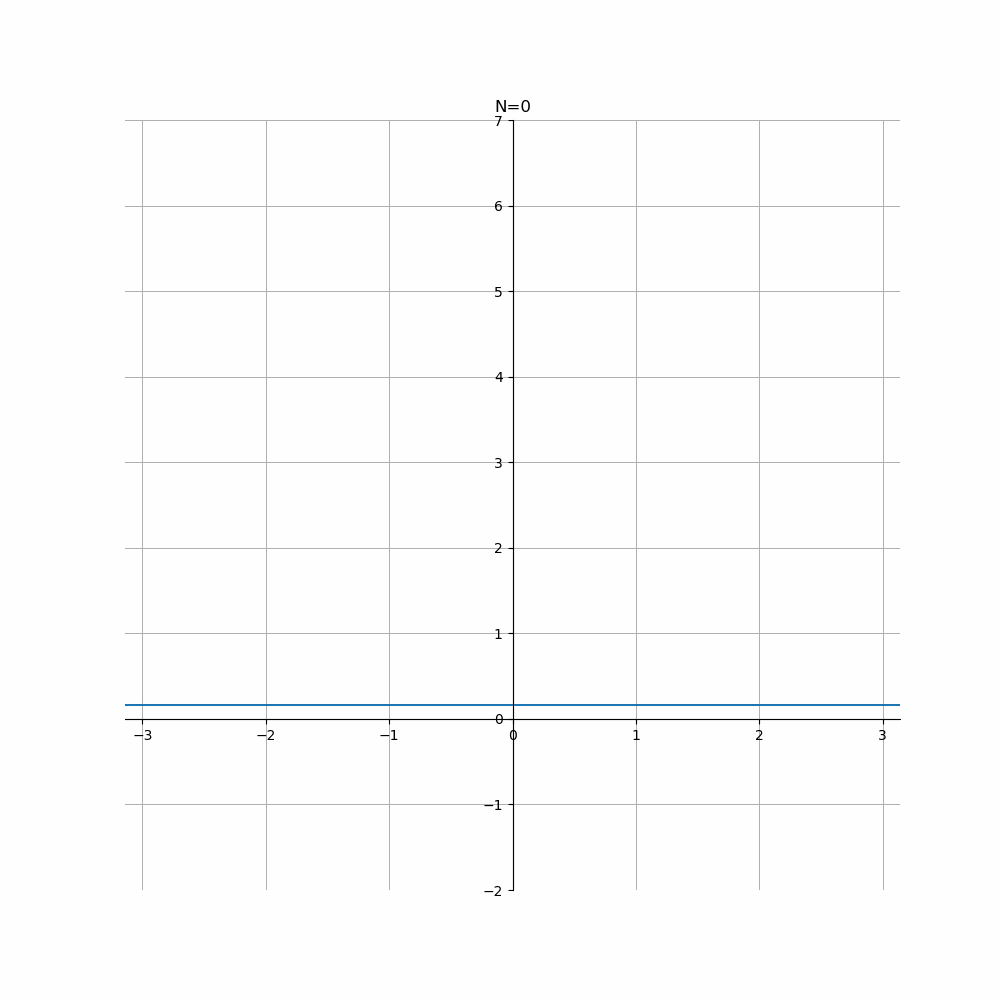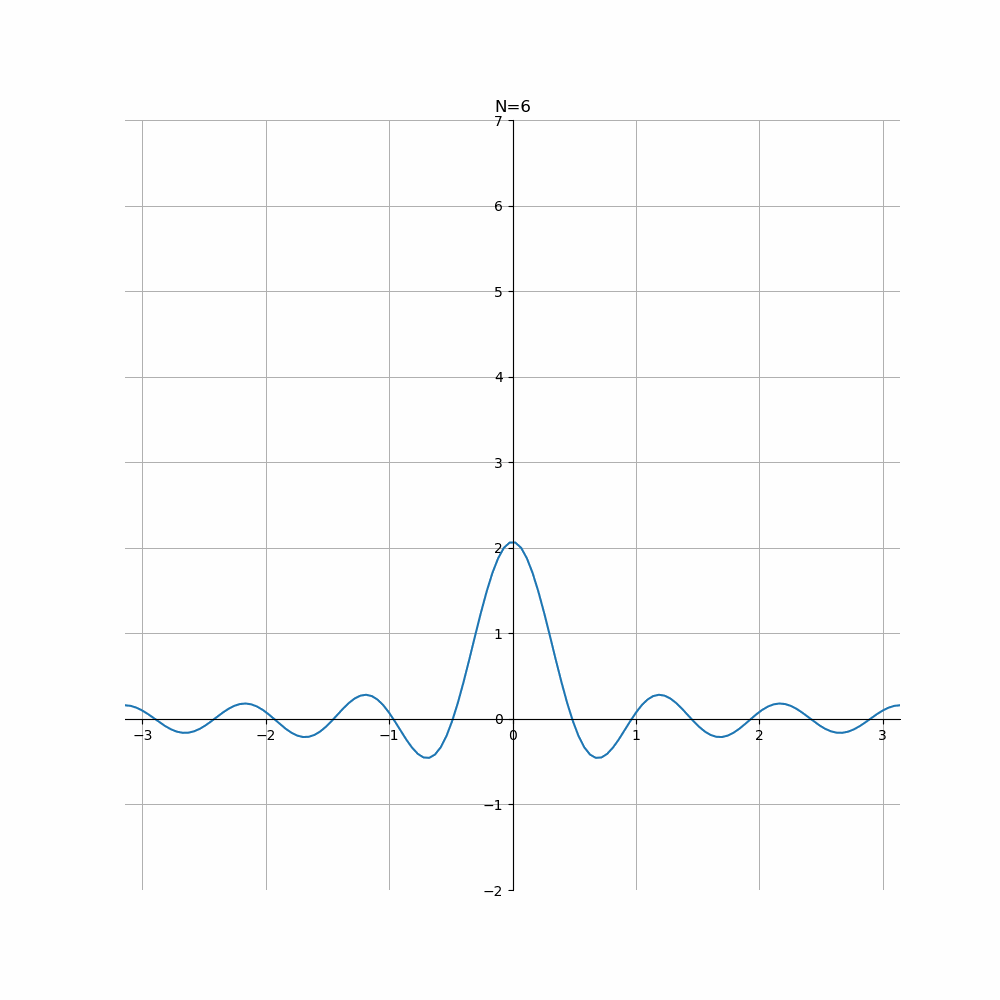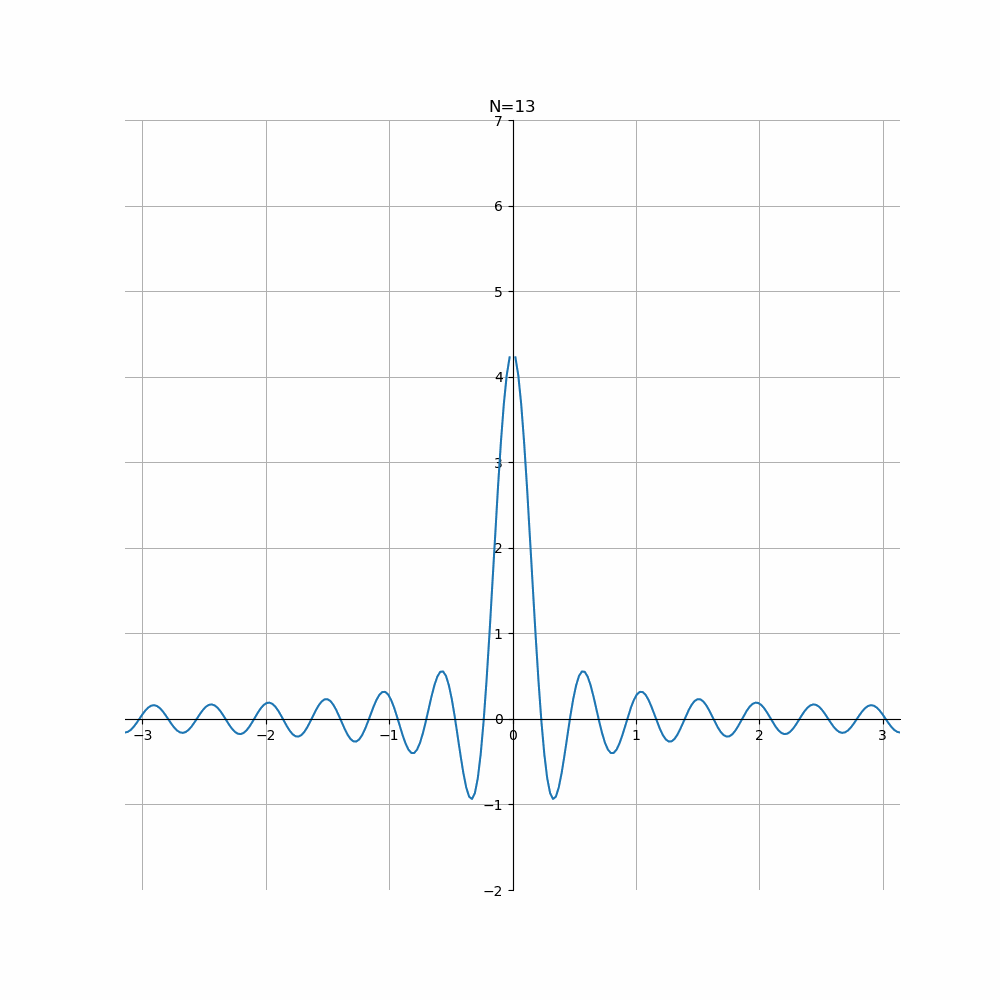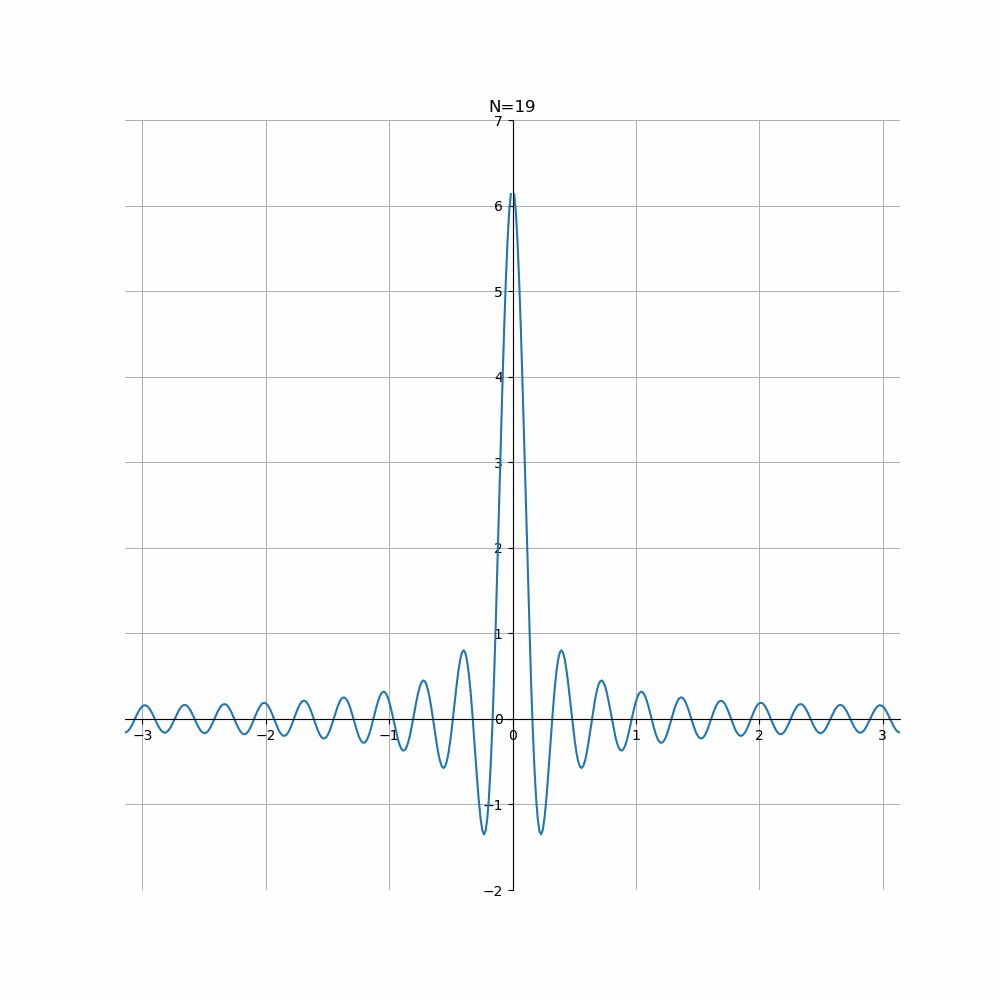
Now
\[S^f_N(\theta = \frac{1}{2\pi} \sum_{-N}^N \int_{-\pi}^\pi f(\psi) e^{in(\psi - \theta)}d\psi = \frac{1}{2\pi} \int^\pi_{-\pi} f(\theta + \phi) D_N(\phi) d\phi\]
where \(D_N(\phi) = \frac{1}{2\pi} \sum_{-N}^N e^{in\phi}\). The function \(D_N (\phi)\) is called the \(N\)-the Dirichlet kernel.As the sum of the finite geometric progression \(D_N(\phi) = \frac{1}{2\pi} e^{iN\phi}\sum_0^{2N} e^{in\phi}\), we have
\[D_N(\phi) = \frac{1}{2\pi}\frac{e^{i(N+1)\phi} - e^{-iN\phi}}{e^{i\phi}-1}.\]
Multiply the numerator and denominator by \(e^{-i\phi/2}\), we obtain
\[D_N(\phi) = \frac{1}{2\pi}\frac{\sin(N+\frac{1}{2})\phi}{\sin \frac{1}{2}\phi}.\]We see from the plot that as \(N\to \infty\), increasingly \(D_N(\phi)\) picks out the value of \(f(\theta + \phi)\) at \(\phi = 0\) (and hence \(f(\theta)\)) in the integral, while away from \(\phi = 0\) rest of the integral are mostly killed off due to the oscillatory cancellation between the positive and negative parts.
Convergence#
Pointwise#
Theorem. If \(f\) is \(2\pi\) periodic and piecewise smooth on \(\mathbb{R}\), then given \(S^f_N\) as above,
\[S^f_N(\theta) = \frac{1}{2}[f(\theta_-) + f(\theta_+))]\]for all \(\theta\). In particular, for every \(\theta\) at which \(f\) is continuous,
\[\lim_{N\to \infty} S^f_N(\theta) = f(\theta).\]Proof. First notice that \(\int_{-\pi}^0 D_N(\theta)d\theta = \int_0^\pi D_N(\theta)d\theta = \frac{1}{2}\). So we have
\[Q_N = S_N^f(\theta) - \frac{1}{2}[f(\theta_- + f(\theta_+))] = \left(\int_{-\pi}^0 + \int_0^\pi\right) D_N(\theta) d\theta\]We wish to show that as \(N\to \infty\), \(Q_N\to 0\).
Use \(D_N(\theta) = \frac{1}{2\pi} \frac{\sin(N+½)\phi}{\sin \phi/2}\) to write \(Q\) as
\[\frac{1}{2\pi}\int_{-\pi}^\pi g(\theta)(e^{i(N+1)\phi}- e^{-iN\phi})d\phi\]where \(g(\phi)\) is given by
\[\frac{f(\theta + \phi)- f(\theta_-)}{e^{i\phi}-1}\]for \(\phi \in (-\pi,0)\), and
\[\frac{f(\theta + \phi)- f(\theta_+)}{e^{i\phi}-1}\]for \(\phi \in (-0,\pi)\). \(g\) is as smooth as \(f\) except near \(\phi = 0\), where by l'Hopital's rule \(\lim_{\phi\to 0_\pm} = -i f'(\theta_\pm)\): \(g\) is piecewise continuous on \([-\pi,\pi]\). Thus its Fourier coefficients \(C_n = \frac{1}{2\pi}\int_{-\pi}^{\pi}g(\theta) e^{-in\phi}d\phi \to 0\) as \(n\to \pm \infty\) from Bessel's inequality.
Now notice that \(Q_N = C_{-(N+1)} - C_N\).
Absolute and Uniform#
Recall that the series \(\sum_1^\infty g_n(x)\) absolutely converges to \(g(x)\) on a set \(S\) if \(\sum_1^\infty |g_n(x)|\) converges for \(x\in S\), and uniformly converges to \(g(x)\) if the quantity
\[\underset{x\in S}{\text{sup}}\left|g(x) - \sum_1^N g_n(x)\right|\]goes to \(0\) as \(N\to\infty\). According to the Weierstrass M-test, if there is a sequence \(M_n\) of positive constants s.t. \(\sum_1^\infty M_n\) is finite and \(|g_n(x)|\leq M_n\) for \(x\in S\), then the series \(\sum_1^\infty g_n(x)\) is absolutely and uniformly convergent.
Theorem. For a \(2\pi\)-periodic, \(C^0\) and \(PC^1\) function \(f\), the Fourier series of \(f\) converges to \(f\) absolutely and uniformly on \(\mathbb{R}\).
Proof. By the M-test, it is sufficient to show that the series \(\sum_{-\infty}^{\infty}|c_n|\) converges. Now first we have
\[\sum_{-\infty}^\infty |c_n| = |c_0| + \sum_{n\neq 0}|\frac{c'_n}{n}| \leq |c_0| + (\sum_{n\neq 0}\frac{1}{n^2})^{½} (\sum_{n\neq 0}|c'_n|^2)^{½}\]where the last equality comes from the Cauchy-Schwarz inequality (we have \(|\frac{c'_n}{n}| = {\frac{{c'_n}^2}{n^2}}^{½}\)) and \(c'_n = in c_n\) is the \(n\)-th Fourier coefficient of \(f'(x)\). Now
\[\sum_{n\neq 0} |c'_n|^2 \leq \sum_{-\infty}^\infty |c'_n|^2 \leq \frac{1}{2\pi} \int_{-\pi}^{\pi} |f'(\theta)|^2 d\theta < \infty\]by Bessel's inequality applied to \(f'\).
It is easy to see that the more derivatives a function has, the more rapidly its Fourier coefficients will tend to zero, and vice versa: \(k\)-th derivative of \(f\), which is \(f^{(k)}\), has Fourier coefficients \(\propto n^k c_n\), and for \(\sum |n^k c_n|\) to be finite (for the derivative to exist) \(|c_n|\) need to decay more rapidly, and for a smooth (i.e. \(C^\infty\)) functions this means that the Fourier coefficients decay more rapidly than any power of \(n\). Recall that a smooth function that has derivatives tending to zero more rapidly than any power of \(n\) is called a Schwartz function; a Schwartz function can be seen as a smooth function whose derivatives of all orders can serve as Fourier coefficients of some smooth function.
However, the proper notion of convergence for Fourier series is \(L^2\)-convergence, for which we need to reformulate Fourier series in the language of Hilbert space.